Motion Estimation using Statistical Learning Theory
This research project studied the novel application of Statistical Learning Theory (SLT) to single motion estimation and tracking. The problem of motion estimation can be related to statistical model selection, where the goal is to select one (correct) motion model from several possible motion models, given finite noisy samples. SLT, also known as Vapnik-Chervonenkis (VC), theory provides analytic generalization bounds for model selection, which have been used successfully for practical model selection. We describes a successful application of an SLT-based model selection approach to the challenging problem of estimating optimal motion models from small data sets of image measurements (flow). The experiment results on both synthetic and real image sequences for motion interpolation and extrapolation demonstrate the feasibility and strength of our approach. Our experimental results show that for motion estimation applications, SLT-based model selection compares favorably against alternative model selection methods, such as the Akaike¡¯s fpe, Schwartz¡¯ criterion (sc), Generalized Cross-Validation (gcv), and Shibata¡¯s Model Selector (sms). The paper also shows how to address the aperture problem using SLT-based model selection for penalized linear (ridge regression) formulation.
Detect Normal Flow

Prediction Risk and Error for Interpolation
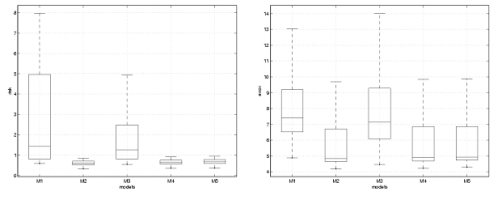
Prediction Risk and Error for Extrapolation

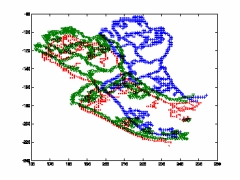
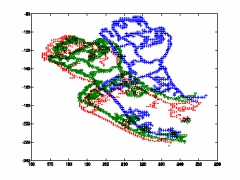
Prediction contour via extrapolation for M2, Affine and Quadratic motion models
|
M2 Model |
Affine Model |
Quadratic Model |
Note: Blue contours are the starting position, green ones are the predicted contours after 2 frames,
and the red ones are the actual contours.