Researchers find a better way to generate origami that can self-fold into highly complex shapes.
by Vinay Bhaip
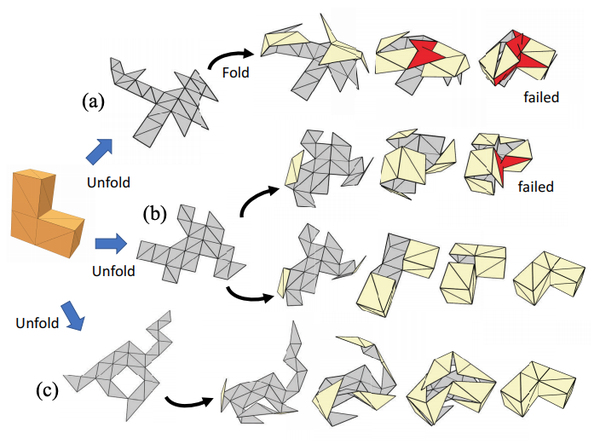
Researcher Yue Hao looks to answer the question of foldability. When a polyhedron is decomposed into different nets, the way that they are folded back can vary significantly. A linearly foldable net is one that has each fold come together at a speed proportional to the folding angle and results in no collisions between different fold pieces. This means that there is a linear collision-free path in the configuration space connecting the flat and folded states. Slightly more challenging than this is the uniformly foldable net in which the pieces all fold together at the same speed.
The problem Hao’s research addresses is how to incorporate the computationally expensive foldability function in an evolution algorithm based optimization process. Hao proposes a fitness function that takes in features such as the number of leaf nodes and hull area to evaluate the extent to which a 2D shape is foldable. This fitness function is used in a genetic algorithm that allows a program to optimize and find solutions to the foldability problem. His research is significant because it addresses the foldability problem in a novel way by transforming the motion planning issue to a geometric and topological one, which allows for an easier way to discover polyhedral nets that satisfy the conditions in the foldability problem.
Hao’s algorithm is also extendable to more complex challenges regarding the foldability problem, when a polyhedron has many faces. Finding a uniformly foldable net for a 128-faced polyhedron, for example, would take a very long time, even using Hao’s optimization. Hao provides a solution for this by breaking down the problem to a simpler one, finding a uniformly foldable net for a 64-faced polyhedron with the same general features. Once his algorithm finds the uniformly foldable net for this simpler polyhedron, it can extend the information it learns to the 128-faced polyhedron, greatly reducing the total time needed to generate the net.
This solution to the foldability problem has important implications in the real world. Generating 2D polyhedral nets that can be folded efficiently allows for a quick process to mass produce certain designs. For example, a special material can be laser-cut as a uniformly foldable polyhedral net that when in contact with heat, such as in an oven, folds into the design. This is why having a uniformly foldable net is crucial because it allows the design to fold without having any intersections at a constant speed. Since the nets are 2D, they can be moved around easily without taking much space, and when the actual folded object is needed, it can be put into an oven. Hao’s research has the ability to significantly influence the field of foldable nets.
