A graph-based method could improve the robustness of finding outliers in data sets, like fraudulent transactions on your credit card bill.
by Ryan Xu
Researchers from George Mason University and the University of Rome are working on a new approach to a problem that involves detecting outliers. The approach was developed by Hamed Sarvari, Carlotta Domeniconi, and Giovanni Stilo. Their work can be found in a paper published in Proceedings of the 34th ACM/SIGAPP Symposium on Applied Computing.
Outliers are data points that do not follow the expected pattern, and they are seen wherever there is data. Being able to determine outliers from a data set is important because it has many practical applications. For example, anomalous behavior might indicate identity theft, or other types of fraud, to credit card companies.
The team’s research and novel idea concerns selective outlier ensembles. Ensembles are used in many areas as a form of machine learning and they achieve a final result by combining aspects of many different algorithms. Some methods weigh every algorithm equally, but these cause poor-performing parts to hurt the final outcome. To combat this, other methods use various factors to eliminate unwanted parts from the combination. The term selective describes this second option. Although ensembles have been studied and applied frequently in a variety of applications, their attention in outlier detection has been relatively low. As a result, there is room for improvement when it comes to the selection process of outlier ensembles.
Outlier ensembles face a unique problem for selecting how to weigh components because the learning is unsupervised. Simply put, unsupervised means that the training mechanism is not allowed to use information about the correct answer. In terms of outliers, the team could not use the data’s known set of outliers in their ensemble approach. As a result, Sarvari says, “in the process of selecting the ensemble components there is no grasp on how successful each outlier detection method is.”
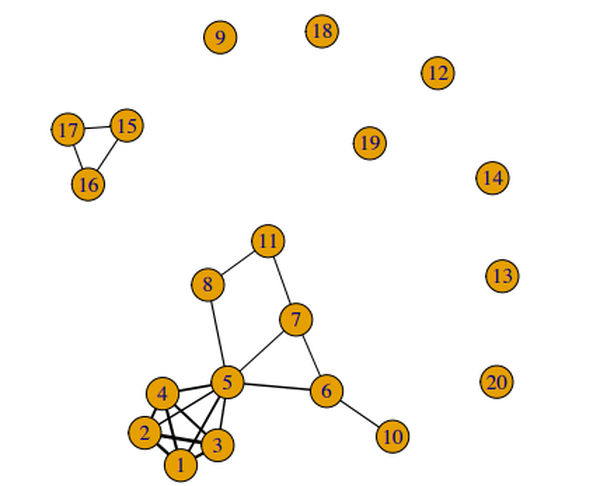
To get around this problem, the team developed a method which relies on analyzing correlation between the parts of the ensemble. They used a well-known statistic called weighted Kendall tau for their measurement of correlation. Knowing this information is helpful because the behavior of ensemble components is somewhat predictable. As Sarvari explains, “accurate components tend to agree on highly ranked objects, but poor components rank various objects high. Therefore, a correlation measure between rankings that emphasizes highly ranked points (like weighted Kendall tau) would show high correlations among accurate components.” This is the fundamental idea behind the team’s graph-based methods, which are the first of their kind. The image above, taken from their published paper, shows the high correlation between the most accurate components.
The current best techniques for selective outlier ensembles include SelectV, SelectH, and DivE. The team designed graph-based methods called Core and Cull.
The team tested their methods using 16 public data sets against the aforementioned current techniques, along with a baseline method All which performed the simplest selection process by including every part. Overall, the experiments produced promising results. Through a well-defined metric and statistical analysis, the team determined the method or methods which performed best for each data set. Of the 16 tests, either their Core or Cull techniques were best in 12. In comparison, SelectV and SelectH were both best in 6, and DivE was best in only 3. This is especially significant because All was best in 9; the team’s methods were the only to outperform the default option, which “is a strong baseline and hard to defeat,” according to the team.
There are still many areas to explore, says the team. From their results, they noticed that Core and Cull performed significantly differently for different data sets. So, one topic of interest is an analysis of situations where each technique outperforms the other. In addition, they look to investigate “hybrid methods.”
